题目内容
如图,C、D是线段AB上任意一点,M为AD的中点,N为CB的中点,如果AB=18cm,CD=8cm,那么MN=________.

5厘米
分析:根据题意,进行推导,求出线段AM+BN的和,然后根据:MN=AB-(AM+BN),代入数据即可得出结论.
解答:因为M为AD的中点,所以AM=DM;
因为N为CB的中点,所以CN=BN;
因为AM+DM+CN+BN-AB=CD,
所以2AM+2BN-AB=CD,
即:2(AM+BN)-18=8,
2(AM+BN)=18+8,
所以AM+BN=13(厘米),
则:MN=AB-(AM+BN)=18-13=5(厘米);
故答案为:5.
点评:本题通过长度之间的等量关系进行转化,求出线段AM+BN的和,是解答此题的关键.
分析:根据题意,进行推导,求出线段AM+BN的和,然后根据:MN=AB-(AM+BN),代入数据即可得出结论.
解答:因为M为AD的中点,所以AM=DM;
因为N为CB的中点,所以CN=BN;
因为AM+DM+CN+BN-AB=CD,
所以2AM+2BN-AB=CD,
即:2(AM+BN)-18=8,
2(AM+BN)=18+8,
所以AM+BN=13(厘米),
则:MN=AB-(AM+BN)=18-13=5(厘米);
故答案为:5.
点评:本题通过长度之间的等量关系进行转化,求出线段AM+BN的和,是解答此题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
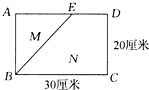 如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小l80平方厘米,那么AE的长是( )
如图,线段BE将长方形ABCD分成M、N两个部分,如果M部分比N部分的面积小l80平方厘米,那么AE的长是( )| A、24厘米 | B、21厘米 | C、20厘米 | D、14厘米 |
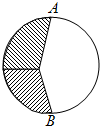 如图,圆的半径是3厘米,A,B是圆上的两个点,图中阴影部分的周长与空白部分的周长相等,则AB线段的长度( )
如图,圆的半径是3厘米,A,B是圆上的两个点,图中阴影部分的周长与空白部分的周长相等,则AB线段的长度( )| A、大于6厘米 | B、小于6厘米 | C、等于6厘米 | D、ABC都有可能 |
 如图,C、D是线段AB上的两点,E是AC的中点,F是BD的中点,若EF=8,CD=4,则AB的长为( )
如图,C、D是线段AB上的两点,E是AC的中点,F是BD的中点,若EF=8,CD=4,则AB的长为( )| A、9 | B、10 | C、12 | D、16 |
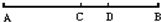 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )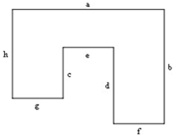 如图,线段a=12厘米,b=9厘米,c=4厘米,d=6厘米,图形的周长是
如图,线段a=12厘米,b=9厘米,c=4厘米,d=6厘米,图形的周长是