题目内容
 如图,AD=DB,AE=EF=FC,已知阴影部分面积为5平方厘米,△ABC的面积是多少平方厘米?
如图,AD=DB,AE=EF=FC,已知阴影部分面积为5平方厘米,△ABC的面积是多少平方厘米?分析:连接BF,因为F、E是三等分点,根据三角形的高一定时,三角形的面积与底的成正比例的性质可得,三角形ABF的面积=
三角形ABC的面积=三角形ADF的面积×2=三角形EDF的面积×4,因为三角形EDF的面积是5平方厘米,由此代入即可解决问题.

| 2 |
| 3 |

解答:解:连接BF,因为F、E是三等分点,根据三角形的高一定时,三角形的面积与底的成正比例的性质可得,三角形ABF的面积=
三角形ABC的面积=三角形ADF的面积×2=三角形EDF的面积×4,
则三角形ABC的面积是:5×4÷
=30(平方厘米);
答:△ABC的面积是30平方厘米.
| 2 |
| 3 |
则三角形ABC的面积是:5×4÷
| 2 |
| 3 |
答:△ABC的面积是30平方厘米.
点评:此题考查了高一定时,三角形的面积与底成正比例的性质的灵活应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
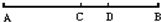 如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )
如图,点C是线段AB的中点,点D是线段CB上任意一点,则下列表示线段关系的式子不正确的是( )