题目内容
如图,把一个大正方形分割成六个小长方形,如果这六个小长方形周长的总和是90厘米,那么原大正方形的面积是
100
100
平方厘米.
分析:根据题意,可知把大正方形分割成六个小长方形,边长比原来增加了3条,这3条边与原正方形的边长相等,在计算每个小长方形的周长时,每相邻的两个小长方形公有的边计算了两次,即在大正方形中共增加了(3×2)条,所以再加上所有的小长方形外围的边组成的4条边长,最后可用90除以六个长方形的边数得出每条边的长度,然后再根据正方形的面积公式计算出正方形的面积即可,列式解答即可得到答案.
解答:解:每条边的长度为:90÷(3×2+4)=10(厘米),
正方形的面积为:10×10=100(平方厘米),
故填:100.
正方形的面积为:10×10=100(平方厘米),
故填:100.
点评:解答此题的关键是确定分割后增加了几条边,这些边与原来正方形的边是否相等,然后再计算出每一条边的长度,最后利用正方形的面积公式进行计算即可.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
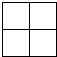 如图所示,把4个边长是5厘米的小正方形拼成一个大正方形,这个大正方形的周长是
如图所示,把4个边长是5厘米的小正方形拼成一个大正方形,这个大正方形的周长是 有一个8×8的大正方形,
有一个8×8的大正方形,
