题目内容
333×334+999×222
+
+
+
+
425÷25
1-0.12+
-0.34+
-0.56+
-0.78
6.73-2
+(3.27-1
)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
425÷25
1-0.12+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
6.73-2
| 8 |
| 17 |
| 9 |
| 17 |
分析:(1)可先将式中999×222根据乘法的性质变为333×3×222=333×666后,再根据乘法分配律计算;
(2)可根据分数巧算公式
=
-
进行巧算;
(3)可根据除法的性质将原式变为425÷5÷5计算;
(4)(5)可根据加法结合律及一个数减几个数,等于减去这几个数的和的减法性质计算.
(2)可根据分数巧算公式
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(3)可根据除法的性质将原式变为425÷5÷5计算;
(4)(5)可根据加法结合律及一个数减几个数,等于减去这几个数的和的减法性质计算.
解答:解:(1)333×334+999×222,
=333×334+333×3×222,
=333×334+333×666,
=333×(334+666),
=333×1000,
=333000;
(2)
+
+
+
+
,
=(1-
)+(
-
)+(
-
)+(
-
),
=1-
+
-
+
-
+
-
,
=1-
,
=
;
(3)425÷25,
=425÷5÷5,
=85÷5,
=17;
(4)1-0.12+
-0.34+
-0.56+
-0.78,
=(1+
+
+
)-(0.12+0.78)-(0.56+0.34),
=2-0.9-0.9.
=0.2;
(5)6.73-2
+(3.27-1
)
=6.73+3.27-(2
+1
),
=10-4,
=6.
=333×334+333×3×222,
=333×334+333×666,
=333×(334+666),
=333×1000,
=333000;
(2)
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
=1-
| 1 |
| 6 |
=
| 5 |
| 6 |
(3)425÷25,
=425÷5÷5,
=85÷5,
=17;
(4)1-0.12+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
=(1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
=2-0.9-0.9.
=0.2;
(5)6.73-2
| 8 |
| 17 |
| 9 |
| 17 |
=6.73+3.27-(2
| 8 |
| 17 |
| 9 |
| 17 |
=10-4,
=6.
点评:完成此类题目要认真分析式中数据的特点及内在联系,然后运用合适的方法进行计算.

练习册系列答案
相关题目
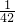 +
+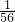 =
= -
- =
= =
= ÷37=
÷37=