题目内容
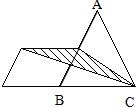
如图,三角形ABC的面试是12平方厘米,且AE=
EC,F是AD的中点.则阴影部分的面积是
| 1 | 2 |
5
5
平方厘米.
分析:此题利用三角形面积与底的正比关系来推算,此题要添加辅助线,即连接CF.如图:


解答:解:因为AE=
EC,所以S△ABE=
S△ABC=12×
=4(平方厘米),S△EBC=
S△ABC.
又因为F是AD的中点,连接FC,所以S△ABF=S△FBD,S△AFC=S△DFC,则有S△ABF+S△AFC=
×12=6(平方厘米).
于是S△EFC=(S△ABF+S△AFC)-S△ABE=6-4=2(平方厘米).
又因为S△AEF=
S△EFC=
×2=1(平方厘米).
而S△DFC=S△AEF+S△EFC=1+2=3(平方厘米),
所以S阴影=S△EFC+S△DFC=2+3=5(平方厘米).
故答案为:5.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
又因为F是AD的中点,连接FC,所以S△ABF=S△FBD,S△AFC=S△DFC,则有S△ABF+S△AFC=
| 1 |
| 2 |
于是S△EFC=(S△ABF+S△AFC)-S△ABE=6-4=2(平方厘米).
又因为S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
而S△DFC=S△AEF+S△EFC=1+2=3(平方厘米),
所以S阴影=S△EFC+S△DFC=2+3=5(平方厘米).
故答案为:5.
点评:此题考查学生对三角形的面积公式的运用掌握情况,以及分析图形的能力.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少?
如图,三角形ABC的面积是16,D是AC的中点,E是BD的中点,那四边形CDEF的面积是多少? 如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=
如图,三角形ABC的面积为10,AD与BF交于点E,且AE=ED,BD=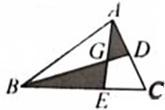 如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积=
如图,三角形ABC的面积是240平方厘米,D是AC的中点,E是BC的三等分点,则阴影部分的面积= 如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.
如图,三角形ABC的面积是20平方厘米,求阴影部分的面积.