题目内容
 如图,BD是梯形ABCD的一条对角线,线段AE与梯形的一条腰DC平行,AE与BD相交于O点.已知三角形BOE的面积比三角形AOD的面积大4平方米,并且EC=
如图,BD是梯形ABCD的一条对角线,线段AE与梯形的一条腰DC平行,AE与BD相交于O点.已知三角形BOE的面积比三角形AOD的面积大4平方米,并且EC= .求梯形ABCD的面积.
.求梯形ABCD的面积.
解:设梯形ABCD的高为H,
因为,AD平行EC,AE平行DC,
所以,AECD是平行四边形,
所以,AD=EC,
又因为,AD平行BE,
△ADO相似△EBO,
又因为,EC= BC,
BC,
所以, =
= ,
,
所以,△ADO高为 H,△EBO高为
H,△EBO高为 H,
H,
又因为:S△EBO-S△ADO=4,
所以,BE× H-AD×
H-AD× H=
H= ×AD×
×AD× H×H-AD×
H×H-AD× H=8,
H=8,
即,AD?H=16,
S梯形ABCD=(AD+BC)×H÷2=(AD+ AD))×H÷2=
AD))×H÷2= AD.H=
AD.H= ×16=28(平方米),
×16=28(平方米),
答:梯形ABCD的面积28平方米.
分析:根据题意,构造相似三角形,找出各个边的关系,利用梯形的面积公式,解答即可.
点评:解答此题的关键是,运用了整体代入的方法,即求出梯形的底与高的乘积,再利用梯形面积公式,计算即可.
因为,AD平行EC,AE平行DC,
所以,AECD是平行四边形,
所以,AD=EC,
又因为,AD平行BE,
△ADO相似△EBO,
又因为,EC=
 BC,
BC,所以,
 =
= ,
,所以,△ADO高为
 H,△EBO高为
H,△EBO高为 H,
H,又因为:S△EBO-S△ADO=4,
所以,BE×
 H-AD×
H-AD× H=
H= ×AD×
×AD× H×H-AD×
H×H-AD× H=8,
H=8,即,AD?H=16,
S梯形ABCD=(AD+BC)×H÷2=(AD+
 AD))×H÷2=
AD))×H÷2= AD.H=
AD.H= ×16=28(平方米),
×16=28(平方米),答:梯形ABCD的面积28平方米.
分析:根据题意,构造相似三角形,找出各个边的关系,利用梯形的面积公式,解答即可.
点评:解答此题的关键是,运用了整体代入的方法,即求出梯形的底与高的乘积,再利用梯形面积公式,计算即可.

练习册系列答案
相关题目
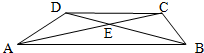 如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( )
如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则( ) 如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积?
如图,在梯形ABCD中,对角线AC、BD相交于O点,OE平行于AB交腰BC于E点,如果三角形OBC的面积是115平方厘米,求三角形ADE的面积? (2012?宜宾县模拟)如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比.
(2012?宜宾县模拟)如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比.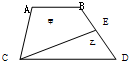 如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比.
如图,ABCD是一个梯形,E是BD的中点,线段CE把梯形分成甲、乙两部分,它们的面积之比是9:5,求上底AB与下底CD的长度之比. 如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则
如图,在梯形ABCD中,CD,AB分别是梯形的上底和下底,AC与BD交于点E,并设三角形ADE的面积是S1,三角形BCE的面积是S2,则