题目内容
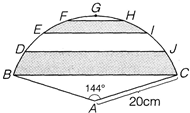 如图为半径20cm、中心角为144°的扇形图.点D、E、F、G、H、I、J是将扇形的B、C弧线分成了8等份的点.求阴影部分的面积之和.(圆周率为3.14)
如图为半径20cm、中心角为144°的扇形图.点D、E、F、G、H、I、J是将扇形的B、C弧线分成了8等份的点.求阴影部分的面积之和.(圆周率为3.14)分析:如下图添加辅助线,要求阴影部分的面积之和,只要求出上下两个阴影部分的面积相加即可.上面阴影的面积就等于扇形AEGI的面积减去弓形FGH的面积,而弓形FGH的面积就等于扇形AFGH的面积减去三角形AFH的面积,如此即可求出上面阴影的面积,同样的办法可求出下面阴影的面积,再相加即可.


解答:解:如上图所示,连接圆心A与圆周上各点,由垂径定理可知,AG与图中所有的弦都垂直;
点D、E、F、G、H、I、J是将扇形的B、C弧线分成了8等份的点,
所以图中每个小的圆心角的度数都是:144°÷8=18°.
S弓形FGH=S扇形AFGH-S△AFH=
×π×202-
×20sin18°×2×20cos18°
=40π-400sin18°cos18°
=40π-200sin36°;
所以上面阴影的面积是:S扇形AEGI-S弓形FGH-S△AEI
=
×π×202-(40π-200sin36°)-
×20sin36°×2×20cos36°
=80π-40π+200sin36°-200sin72°
=40π+200sin36°-200sin72°;
S弓形DGJ=S扇形ADGJ-S△ADJ
=
×π×202-
×20sin54°×2×20cos54°
=120π-200sin108°;
所以下面阴影的面积是:S扇形ABGC-S弓形DGJ-S△ABC
=
×π×202-(120π-200sin108°)-
×20sin72°×2×20cos72°
=160π-120π+200sin108°-200sin144°
=40π+200sin108°-200sin144°;
所以阴影部分的面积之和是:40π+200sin36°-200sin72°+40π+200sin108°-200sin144°
=80π
=80×3.14
=251.2(cm2);
答:阴影部分的面积之和是251.2cm2.
点D、E、F、G、H、I、J是将扇形的B、C弧线分成了8等份的点,
所以图中每个小的圆心角的度数都是:144°÷8=18°.
S弓形FGH=S扇形AFGH-S△AFH=
| 18×2 |
| 360 |
| 1 |
| 2 |
=40π-400sin18°cos18°
=40π-200sin36°;
所以上面阴影的面积是:S扇形AEGI-S弓形FGH-S△AEI
=
| 18×4 |
| 360 |
| 1 |
| 2 |
=80π-40π+200sin36°-200sin72°
=40π+200sin36°-200sin72°;
S弓形DGJ=S扇形ADGJ-S△ADJ
=
| 18×6 |
| 360 |
| 1 |
| 2 |
=120π-200sin108°;
所以下面阴影的面积是:S扇形ABGC-S弓形DGJ-S△ABC
=
| 144 |
| 360 |
| 1 |
| 2 |
=160π-120π+200sin108°-200sin144°
=40π+200sin108°-200sin144°;
所以阴影部分的面积之和是:40π+200sin36°-200sin72°+40π+200sin108°-200sin144°
=80π
=80×3.14
=251.2(cm2);
答:阴影部分的面积之和是251.2cm2.
点评:本题解决的思路简单,但是过程比较复杂.用到的公式有:sin2a=2sinacosa;sinA=sin(180-A).

练习册系列答案
相关题目
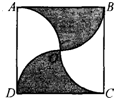 如图,正方形ABCD的边长是20cm,
如图,正方形ABCD的边长是20cm,
 如图,正方形ABCD的边长是20cm,
如图,正方形ABCD的边长是20cm, ,
,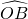 ,
,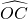 ,
, 分别是以各边中点为圆心,半径是10cm的圆弧.则阴影部分的面积是________cm2.
分别是以各边中点为圆心,半径是10cm的圆弧.则阴影部分的面积是________cm2.