Question

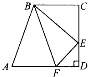
右面的直角梯形中，已知梯形上底6cm，下底9cm，高8cm，三角形ABF、三角形BCE和四边形BEDF面积相等，三角形BEF的面积是

17

1

3

cm²．

Answer 1

分析：三角形ABF、三角形BCE和四边形BECF把梯形平均分成了3部分，根据梯形的面积求出求出四边形AECF面积，再根据三角形ABF、三角形BCE的面积求出ED和DF的长度，进而求出三角形EFD的面积；用四边形BEDF面积-三角形EFD的面积就是三角形BEF的面积．

解答：解：梯形的面积：（6+9）×8÷2=60（平方厘米），
60÷3=20（平方厘米），
CE=20×2÷6=6

2

3

（厘米），
ED=8-6

2

3

=1

1

3

（厘米），
AF=20×2÷8=5（厘米），
FD=9-5=4（厘米），
S△BEF=SBEDF-S△EFD，
=20-4×1

1

3

÷2，
=20-4×

4

3

×

1

2

，
=20-2

2

3

，
=17

1

3

（平方厘米），
答：三角形BEF的面积是17

1

3

平方厘米．
故答案为：17

1

3

．

点评：本题关键是找出要求的面积是用哪些面积求解，分别求出需要的面积后再根据图形之间的面积关系求解．