题目内容
9.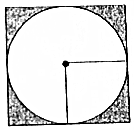 如下图.阴影部分的面积与正方形的面积比值是$\frac{4-π}{4}$.
如下图.阴影部分的面积与正方形的面积比值是$\frac{4-π}{4}$.
分析 假设圆的半径为r,则正方形的边长为2r,阴影部分的面积等于正方形的面积减去圆的面积,因此利用正方形和圆的面积公式分别求出正方形和阴影部分的面积,再求它们的面积比即可.
解答 解:设圆的半径为r,则正方形的边长为2r,
正方形的面积:2r×2r=4r2,
阴影部分的面积:4r2-πr2=(4-π)r2,
阴影部分的面积与正方形的面积比值是:
(4-π)r2:4r2
=(4-π):4
=$\frac{4-π}{4}$.
答:阴影部分的面积与正方形的面积比值是 $\frac{4-π}{4}$.
故答案为:$\frac{4-π}{4}$.
点评 此题主要考查正方形和圆的面积公式的灵活应用.

练习册系列答案
相关题目
17.计算.
| 148+57= | 30×800= | 125×8÷100= | 48×25= |
| 370-201= | 12.7万-5万= | 2.3×100÷10= | 4.8+0.2-48+0.2= |
14.用两个长5厘米,宽4厘米,高2厘米的长方体拼成一个大长方体,表面积最大是( )平方厘米.
| A. | 152 | B. | 116 | C. | 112 | D. | 136 |
19.小花猫( )爱吃鱼.
| A. | 不可能 | B. | 可能 | C. | 一定 |
