题目内容
如图,一个正方形ABCD内有两条直线AE、AF,边AD沿AE折叠后恰好落在正方形的对角线AC上,边AB沿AF折叠后恰好落在AE上,通过两次折叠得到一个不规则的四边形AFCE,则∠FAE= .


分析:由于边AD沿AE折叠后恰好落在正方形的对角线AC上,所以∠DAE=∠CAE=
∠DAB=
×90°=22.5°,所以∠BAE=90°-22.5°=67.5°,又由于边AB沿AF折叠后恰好落在AE上,所以∠BAF=∠EAF=
∠BAE=
×67.5°=33.75°,∠BAE就是通过两次折叠得到一个不规则的四边形AFCE的∠FAE,问题得到解答.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由正方形的折叠可知,
∠DAE=∠CAE=
∠DAB=
×90°=22.5°,
∠FAE=∠BAF=∠EAF=
∠BAE=
×67.5°=33.75°;
故答案为:33.75°
∠DAE=∠CAE=
| 1 |
| 4 |
| 1 |
| 4 |
∠FAE=∠BAF=∠EAF=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:33.75°
点评:通过正方形的折叠可知,∠FAE就是正方形的一个角(90°)减去正方形角的
的
.
| 1 |
| 4 |
| 1 |
| 2 |

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
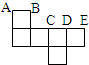 (2006?徐州)如图是一个正方形纸盒的展开图,当折叠成正方体纸盒时,C点与( )点重合.
(2006?徐州)如图是一个正方形纸盒的展开图,当折叠成正方体纸盒时,C点与( )点重合.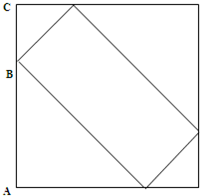 如图.一个正方形中套着一个长方形.已知正方形边长是24厘米,AB=3BC.求长方形的面积是多少?
如图.一个正方形中套着一个长方形.已知正方形边长是24厘米,AB=3BC.求长方形的面积是多少?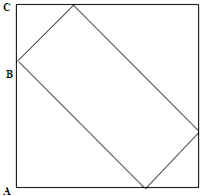 如图.一个正方形中套着一个长方形.已知正方形边长是24厘米,AB=3BC.求长方形的面积是多少?
如图.一个正方形中套着一个长方形.已知正方形边长是24厘米,AB=3BC.求长方形的面积是多少?