题目内容
不能密铺．√
√
．分析：在平面镶嵌时必须满足密铺，即几个内角合起来必须为360°，而正多边形的每个内角相等，所以必须满足正多边形的一个内角能整除360°，正五边的开的每个内角是108°，不能整除360°，不能密铺．
解答：解：如图，
正五边形每个内角的度数是：（5-2）×180°÷5=3×180°÷5=108°，
360÷108=
，即108不能整除360，
因此，正五边形不能密铺；
故答案为：√
正五边形每个内角的度数是：（5-2）×180°÷5=3×180°÷5=108°，
360÷108=
| 10 |
| 3 |
因此，正五边形不能密铺；
故答案为：√
点评：本题考查了平面镶嵌（密铺），几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．
练习册系列答案
巧学巧练系列答案
相关题目
下面图形中哪个不能密铺？（ ）
A、 | B、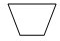 | C、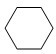 | D、 |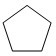
下列图形，不能“密铺”的是（ ）
A、 | B、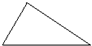 | C、 |