题目内容
 如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是________.
如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是________.
9:8
分析:设△DEC的面积、△ABC的面积分别为S1及S2,将它们分别等分为4个、9个等腰直角三角形,可得:
S阴影= S1,S阴影=
S1,S阴影= S2,因为
S2,因为 S1=
S1= S2,然后根据比例的基本性质逆运算求出S1和S2的比.
S2,然后根据比例的基本性质逆运算求出S1和S2的比.
解答:如图:

S阴影= S1,S阴影=
S1,S阴影= S2,因为
S2,因为 S1=
S1= S2,
S2,
则:S2:S1= :
: =9:8;
=9:8;
故答案为:9:8.
点评:解答此题应根据比例基本性质的逆运算进行解答.
分析:设△DEC的面积、△ABC的面积分别为S1及S2,将它们分别等分为4个、9个等腰直角三角形,可得:
S阴影=
 S1,S阴影=
S1,S阴影= S2,因为
S2,因为 S1=
S1= S2,然后根据比例的基本性质逆运算求出S1和S2的比.
S2,然后根据比例的基本性质逆运算求出S1和S2的比.解答:如图:

S阴影=
 S1,S阴影=
S1,S阴影= S2,因为
S2,因为 S1=
S1= S2,
S2,则:S2:S1=
 :
: =9:8;
=9:8;故答案为:9:8.
点评:解答此题应根据比例基本性质的逆运算进行解答.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 如图,三角形ABC和三角形DEF分别是等腰直角三角形.已知DF=6,AB=5,EB=2.6,则阴影部分的面积是
如图,三角形ABC和三角形DEF分别是等腰直角三角形.已知DF=6,AB=5,EB=2.6,则阴影部分的面积是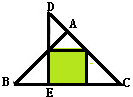 (2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是
(2013?北京模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是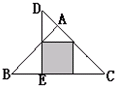 如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是
如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC与三角形DEC的面积比是 (2007?淮安模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC和三角形DEC的面积比是( )
(2007?淮安模拟)如图,三角形ABC和三角形DEC都是等腰直角三角形,阴影部分是正方形,三角形ABC和三角形DEC的面积比是( ) 如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是________平方米.
如图,三角形ABC和三角形DEC都是等腰直角三角形,A和E是直角等点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是________平方米.