题目内容
在周长相等的圆、正方形和长方形中,面积最大的是长方形.
×
×
.(判断对错)分析:周长相等的圆、正方形和长方形,谁的面积最大,谁的面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
解答:解:为了便于理解,假设圆、正方形和长方形的周长都是16,
则圆的面积为:
=20.38;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的圆、正方形和长方形,圆面积最大.
故答案为:×.
则圆的面积为:
| 16×16 |
| 4π |
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的圆、正方形和长方形,圆面积最大.
故答案为:×.
点评:记住结论:周长相等的平面图形,圆的面积最大.

练习册系列答案
相关题目
 是1亩田的
是1亩田的 .
.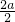 +3a=2+
+3a=2+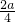 +3a,a是自然数.
+3a,a是自然数.