题目内容
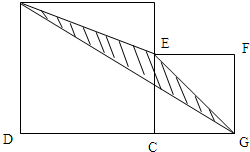 如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其中D、C、G在同一条直线上,小正方形ECGF的边长为6,连AE、EG、AG,求图中阴影部分的面积.
如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其中D、C、G在同一条直线上,小正方形ECGF的边长为6,连AE、EG、AG,求图中阴影部分的面积.分析:如图所示,连接AC,三角形AEC与三角形ACG等底等高,则它们的面积相等,于是它们都减去公共部分三角形AHC,则剩余的部分仍然相等,即三角形AEH与三角形HCG的面积相等,由此可以得出:阴影部分的面积=
×小正方形的面积,小正方形的边长,从而问题得解.

| 1 |
| 2 |

解答:解:连接AC,
则S△AEC=S△ACG,
S△AEC-S△AHC=S△ACG-S△AHC,
即S△AEH=S△HCG,
所以阴影部分的面积=
×6×6,
=3×6,
=18;
答:图中阴影部分的面积是18.
则S△AEC=S△ACG,
S△AEC-S△AHC=S△ACG-S△AHC,
即S△AEH=S△HCG,
所以阴影部分的面积=
| 1 |
| 2 |
=3×6,
=18;
答:图中阴影部分的面积是18.
点评:解答此题的关键是作出合适的辅助线,将阴影部分转化到小正方形中,从而问题得解.

练习册系列答案
相关题目
 (2012?汨罗市模拟)某车间为了能高质量准时完成一批齿轮订单,对车间工人提前进行了加工齿轮效率的测试,经过统计测算,平均每个工人加工齿轮效率情况如图:
(2012?汨罗市模拟)某车间为了能高质量准时完成一批齿轮订单,对车间工人提前进行了加工齿轮效率的测试,经过统计测算,平均每个工人加工齿轮效率情况如图: 阅读以下两则材料,并完成后面的4个问题.
阅读以下两则材料,并完成后面的4个问题.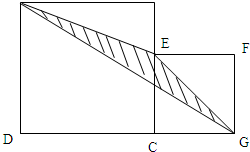 如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其中D、C、G在同一条直线上,小正方形ECGF的边长为6,连AE、EG、AG,求图中阴影部分的面积.
如果你完成上述题目觉得正确无误后,可考虑解决以下问题,注意:本题不计入总分.两个正方形如图放置,其中D、C、G在同一条直线上,小正方形ECGF的边长为6,连AE、EG、AG,求图中阴影部分的面积.