题目内容
 下面的乘法算式中,每个字母都是1~9中的数字,且不同的字母代表不同的数字,相同的字母代表相同的数字,己知E=4,P=5,那么,四位数ABCD=
下面的乘法算式中,每个字母都是1~9中的数字,且不同的字母代表不同的数字,相同的字母代表相同的数字,己知E=4,P=5,那么,四位数ABCD=1963
1963
.分析:根据E=4,且乘积是四位数,可得A最大是2,又因为积的十位数字是5,根据4的乘法口诀可得:D=3,C=6正好满足P=5,此时O=2,还剩下1、7、8、9,经过计算可得,B=9,A=1,此时M=7,N=8,据此即可解答.
解答:解:根据题干分析可得:
1963
1963×4=7852,
所以四位数ABCD=1963.
故答案为:1963.
1963
| × 4 |
| 7852 |
1963×4=7852,
所以四位数ABCD=1963.
故答案为:1963.
点评:本题考查学生的乘法的计算熟练程度,能激起学生学习的兴趣,是个好题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 在下面乘法算式中,每一方框要填一个数字,若一个汉字代表一个数字,不同汉字代表不同的数字.请问最后的积(五位数)是多少?
在下面乘法算式中,每一方框要填一个数字,若一个汉字代表一个数字,不同汉字代表不同的数字.请问最后的积(五位数)是多少?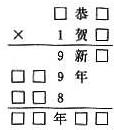 在下面乘法算式中,每一个方框里要填一个数字;每一个汉字代表一个数字,不同的汉字代表不同的数字,相同的汉字代表相同的数字,那么,这个乘法算式的最后乘积是
在下面乘法算式中,每一个方框里要填一个数字;每一个汉字代表一个数字,不同的汉字代表不同的数字,相同的汉字代表相同的数字,那么,这个乘法算式的最后乘积是