题目内容
 两个长方形和一个小正方形拼成了一个大正方形,两个长方形的面积分别是21cm2和12cm2,则大正方形的面积是
两个长方形和一个小正方形拼成了一个大正方形,两个长方形的面积分别是21cm2和12cm2,则大正方形的面积是分析: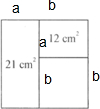 设大长方形的宽是a厘米,小正方形的边长是b厘米,如右图:那么小长方形的长就是小正方形的边长b厘米,小长方形的宽是a厘米;大正方形的边长就是(a+b)厘米,也就是大长方形的长是(a+b)厘米;分别用a、b表示出大长方形和小长方形的面积,然后相减就可以得出a的值,进而求出b的值,以及大正方形的面积.
设大长方形的宽是a厘米,小正方形的边长是b厘米,如右图:那么小长方形的长就是小正方形的边长b厘米,小长方形的宽是a厘米;大正方形的边长就是(a+b)厘米,也就是大长方形的长是(a+b)厘米;分别用a、b表示出大长方形和小长方形的面积,然后相减就可以得出a的值,进而求出b的值,以及大正方形的面积.
 设大长方形的宽是a厘米,小正方形的边长是b厘米,如右图:那么小长方形的长就是小正方形的边长b厘米,小长方形的宽是a厘米;大正方形的边长就是(a+b)厘米,也就是大长方形的长是(a+b)厘米;分别用a、b表示出大长方形和小长方形的面积,然后相减就可以得出a的值,进而求出b的值,以及大正方形的面积.
设大长方形的宽是a厘米,小正方形的边长是b厘米,如右图:那么小长方形的长就是小正方形的边长b厘米,小长方形的宽是a厘米;大正方形的边长就是(a+b)厘米,也就是大长方形的长是(a+b)厘米;分别用a、b表示出大长方形和小长方形的面积,然后相减就可以得出a的值,进而求出b的值,以及大正方形的面积.解答:解:设大长方形的宽是a厘米,小正方形的边长是b厘米;
大长方形的面积就是(a+b)×a,也就是a2+ab=21①;
小长方形的面积就是ab=12②.
用①-②可得:
a2+ab-ab=21-12
a2=9
所以:a=3;
b=12÷a=12÷3=4(厘米);
大正方形的面积是:
(3+4)×(3+4)
=7×7
=49(平方厘米);
答:大正方形的面积是 49平方厘米.
故答案为:49平方厘米.
大长方形的面积就是(a+b)×a,也就是a2+ab=21①;
小长方形的面积就是ab=12②.
用①-②可得:
a2+ab-ab=21-12
a2=9
所以:a=3;
b=12÷a=12÷3=4(厘米);
大正方形的面积是:
(3+4)×(3+4)
=7×7
=49(平方厘米);
答:大正方形的面积是 49平方厘米.
故答案为:49平方厘米.
点评:本题关键是根据大正方形、小正方形、以及两个长方形边长之间的关系,求出大正方形的边长,从而得解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



