题目内容
不同的余数有多少个?
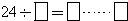
①余数共有 个;
②不同的余数共有 个.
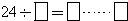
①余数共有
②不同的余数共有
分析:把1~24作为除数都代入:被除数÷除数=商…余数,然后分别求出,里面的技巧是:除数为:1、2、3、4、6、8、12、24时,余数为零不用算,继而数出不同的余数即可.
解答:解:24÷(5 )=( 4)…(4 )
24÷( 7)=( 3)…(3 )
24÷( 9)=( 2)…(6 )
24÷(10)=( 2)…(4 )
24÷( 11)=(2)…(2 )
24÷( 13)=( 1)…(11 )
24÷( 14)=( 1)…(10 )
24÷( 15)=( 1)…(9 )
24÷( 16)=( 1)…(8 )
24÷( 17)=( 1)…(7 )
24÷( 18)=( 1)…(6)
24÷( 19)=( 1)…(5 )
24÷( 20)=( 1)…(4 )
24÷( 21)=( 1)…(3 )
24÷( 22)=( 1)…(2 )
24÷( 23)=( 1)…(1 )
余数共有( 16)个,其中不相同的余数有11个;
故答案为:16,11.
24÷( 7)=( 3)…(3 )
24÷( 9)=( 2)…(6 )
24÷(10)=( 2)…(4 )
24÷( 11)=(2)…(2 )
24÷( 13)=( 1)…(11 )
24÷( 14)=( 1)…(10 )
24÷( 15)=( 1)…(9 )
24÷( 16)=( 1)…(8 )
24÷( 17)=( 1)…(7 )
24÷( 18)=( 1)…(6)
24÷( 19)=( 1)…(5 )
24÷( 20)=( 1)…(4 )
24÷( 21)=( 1)…(3 )
24÷( 22)=( 1)…(2 )
24÷( 23)=( 1)…(1 )
余数共有( 16)个,其中不相同的余数有11个;
故答案为:16,11.
点评:此题应明确:余数总比除数小,然后根据被除数、除数、商和余数之间的关系进行解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目