Question

70名学生参加体育比赛，短跑得奖的31人，投掷得奖的36人，弹跳得奖的29人，短跑与投掷二项均得奖的12人，跑、跳、投三项均得奖的有5人，只得弹跳奖的有7人，只得投掷奖的有15人．求：
（1）只得短跑奖的人数；
（2）得二项奖的总人数；
（3）一项奖均未得的人数．

Answer 1

分析：此题的数量关系比较复杂，可以借助图帮助我们分析，根据容斥原理，找出数量关系等式，列式解答即可．

解答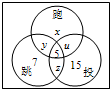：解：（1）只在短跑和弹跳两项得奖的人数：36-15-12+5=14（人），
只在弹跑与投掷两项得奖的人数：29-7-14+5=13，
只得短跑奖的人数：36-12-13+5=16（人）；
（2）得二次奖的人数为：12+14+13-5-5=24（人），
（3）一项奖均未得的人数为：70-36-15-7-14+5=3（人）；
答：只得短跑奖的人数是16人，得二项奖的总人数是24人，一项奖均未得的人数是3人．

点评：解答此题的关键是，弄清题意，找出对应量，根据容斥原理，列式解答即可．