Question

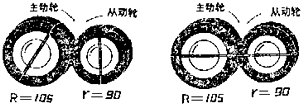有一对紧贴的传动胶轮，每个轮子上都画有一条通过轴心的标志线（如图）．主动轮的半径是105 厘米，从动轮的半径是90厘米．开始转动时，两个轮子上的标志线在一条直线上．问：主动轮至少转了几转后，两轮的标志线又在一条直线上？

Answer 1

分析：要想保证两轮的标志线在同一直线，这必须保证两轮的标志线的同一点．设主动轮轮转n圈，则主动轮转了n.2π×105的距离，于是整数，约分后得

7n

3

，说明n至少取3，

7n

3

才是整数，才能满足要求．

解答：解：设主动轮转n圈，则主动轮转了n.2π×105的距离，
于是有

n×2π×105

90π

，且是整数，
约分后：

n×2π×105

90π

=

7n

3

说明n至少取3，

7n

3

才是整数；
答：主动轮至少转了3圈后，两条标志线又在同一直线上．

点评：解决此题的关键是将主动轮与从动轮转的距离相比，为保证结果是整数，从而推得最少圈数．