Question

在边长为1厘米的正方形ABCD中，分别以A、B、C、D为圆心，1厘米为半径画四分之一圆，交点E、F、G、H，如图，则中间阴影部分的周长为

2.094

厘米．（取圆周率π=3.141）

Answer 1

分析：如图所示：由题意很容易就可以得出△_ABF为等边三角形，则弧

AGF

为

1

6

圆，同理弧

FGC

也为

1

6

圆，所以弧

GF

=

AGF

+

FGC

-

AGC

=

1

12

圆，同理其余三段也为

1

12

圆，故周长=

1

3

圆，再据圆的周长公式即可得解．

解答：解：依题易知△ABF为等边三角形，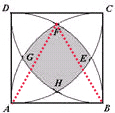
故弧

AGF

为

1

6

圆，同理弧

FGC

也为

1

6

圆，
所以弧

GF

=

AGF

+

FGC

-

AGC

=

1

12

圆，
同理其余三段也为

1

12

圆，
故阴影部分的周长
=

1

12

圆×4
=

1

3

圆
=

2×1×π

3

=2.094（厘米）；
答：中间阴影部分的周长为 2.094厘米．

点评：解答此题的关键是：推论得出其中一段弧长等于半径为1厘米的圆的周长的

1

12

，问题即可逐步得解．