Question

小乌龟和小兔赛跑，比赛场地从起点到插小红旗处为104米．比赛规定：小兔从起点出发跑到小红旗处立即返回，跑到起点处再立即返回…已知小兔每秒跑10.2米，小乌龟每秒爬0.2米．如果从起点同时出发算它们第1次相遇（同时到达同一地点就叫相遇），那么，
（1）出发后多长时间它们第2次相遇？
（2）它们第3次相遇时距起点有多远？

Answer 1

分析：（1）由从起点同时出发算它们第1次相遇（同时到达同一地点就叫相遇），则第2次相遇时，它们共走了2个路程，由追及问题变成相遇问题，就用总路程除以速度和就是出发后第2次相遇的时间104×2÷（10.2+0.2）=20秒；
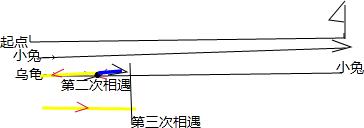
（2））它们第3次相遇时，又从相遇点开始变成小兔追乌龟则小兔走的路程应包括乌龟已走路程的2倍加上与小兔同时间走的路程，列方程求出时间，再用乌龟的是的乘以时间就是距起点的距离．如图：

解答：解：（1）出发后第2次相遇的时间：
104×2÷（10.2+0.2），
=208÷10.4，
=20秒；
答：出发后20秒它们第2次相遇；
（2）设第三次相遇时用了x小时，则：
10.2x=4+4+0.2x，
10.2x-0.2x=4+4+0.2x-0.2x，
10x=8，
x=0.8，
0.2×（20+0.8）=4.16（米），
答：它们第3次相遇时距起点有4.16米．

点评：此题主要抓住由从起点同时出发算它们第1次相遇，则第2次相遇时，它们共走了2个路程，就可根据路程除以速度和求出时间；从图又发现第三次相遇是追及问题，找到等量关系用方程解答．