题目内容
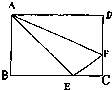
如图，在图中△ABE、ADF和四边形AECF面积相等．阴影部分的面积是多少？分析：因为图中△ABE、ADF和四边形AECF面积相等，因此可以用长方形ABCD的面积除以3得到△ABE、ADF和四边形AECF的面积；然后利用三角形的面积公式，已知三角形的面积和高，可以求出三角形的底，即BE和DF的长度，进而求出EC和CF的长度，然后利用三角形的面积公式求出三角形FEC的面积，再用四边形AECF的面积减去三角形FEC的面积即可．
解答：解：△ABE、ADF和四边形AECF的面积是：6×9÷3=18（平方厘米），
BE=18×2÷6=6（厘米），
DF=18×2÷9=4（厘米），
所以CE=BC-BE=9-6=3（厘米），
CF=CD-DF=6-4=2（厘米），
所以三角形FEC的面积是：3×2÷2=3（平方厘米），
因此阴影部分的面积是：18-3=15（平方厘米）；
答：阴影部分的面积是15平方厘米．
BE=18×2÷6=6（厘米），
DF=18×2÷9=4（厘米），
所以CE=BC-BE=9-6=3（厘米），
CF=CD-DF=6-4=2（厘米），
所以三角形FEC的面积是：3×2÷2=3（平方厘米），
因此阴影部分的面积是：18-3=15（平方厘米）；
答：阴影部分的面积是15平方厘米．
点评：解决本题的关键是求出△ABE、ADF和四边形AECF面积，并能灵活的利用三角形的面积公式求得某些线段的长度．
练习册系列答案
相关题目
如图：在梯形ABCD中，AB=4厘米，CD=9厘米，△ABE的面积是10平方厘米米，求阴影部分的面积．
如图，在矩形ABCD中，点E，F分别在BC，CD上，将△ABE沿AE折叠，使点B落在AC上的点B′处，又将△CEF沿EF折叠，使点C落在EB′与AD的交点C′处．则BC：AB的值为
如图在长方形ABCD中，△ABE、△ADF、四边形AECF的面积相等．△AEF的面积是长方形ABCD面积的