��Ŀ����
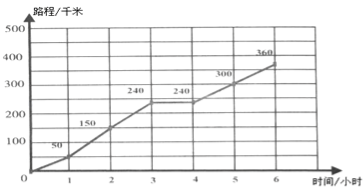
����Ŀ����4�֣���ͼ���������ܵ����ܳ�Ϊ360�ף��ס�������ͬʱ���������ܵ���A���������˳ʱ�뷽���н������ٶ�ʼ��Ϊ5��/�룻��������ٶ�Ϊ6��/�룬��һ�ι�����ٶȼ���![]() ���ڶ��ι�����ٶ�����
���ڶ��ι�����ٶ�����![]() �������ι�����ٶȼ���
�������ι�����ٶȼ���![]() �����Ĵι�����ٶ�����
�����Ĵι�����ٶ�����![]() �������ȥ�����ʣ������������ס������˵�1�������������ص��ںδ�����������������ǵ�100�������������ص��ںδ�����ע�⣺������һ��Ϊ��������
�������ȥ�����ʣ������������ס������˵�1�������������ص��ںδ�����������������ǵ�100�������������ص��ںδ�����ע�⣺������һ��Ϊ��������

���𰸡�������30���ס������˵�1�������������ص������D60�״���������360000�����ǵ�100�������������ص��ڵ�A����
��������
����������ҵ��ٶ�6����1��![]() ��=4��4��
��=4��4��![]() =6���ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6��A��Dʱ����D����18�룬������15�룬���ٶȱ�Ϊ4��/�룬����C��36�룬�ҵ���C��15+90��4=37.5�룬���Ե�һ������һ�����߶�DC��ijһ��������
=6���ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6��A��Dʱ����D����18�룬������15�룬���ٶȱ�Ϊ4��/�룬����C��36�룬�ҵ���C��15+90��4=37.5�룬���Ե�һ������һ�����߶�DC��ijһ��������
�ݴ������ڶ������߶�BC�ϵ��е�������
���������߶�AB�����A60�״�������
���Ĵ�ǡ���ڵ�D���������Ӵ˿�ʼ���������ң�����Ҫ��������ֻ���Ǽױ��Ҷ���һȦ���ݴ˽�ɣ�
�⣺��1���ҵ��ٶȣ�
6����1��![]() ��=4����/�룩��
��=4����/�룩��
4��![]() =6����/�룩��
=6����/�룩��
�����ҵ��ٶ���A��D��C��B��A���仯���£�6��4��6��4��6
360��4=90���ף�
90��5=18���룩
90��6=15���룩
90��4=22.5���룩
�״ӵ�A����C�ã�18��2=36���룩��
�Ҵӵ�A����C�ã�15+22.5=37.5���룩
���Լ�������һ�����߶�DC��ijһ��������
��x���һ��������������ã�
90+5��x��18��=90+4��x��15��
��ã�x=30
30��5=150���ף�
150��90=60���ף�
�𣺳�����30���ס������˵�1�������������ص������D60�״���
��2����1��������DC�ϣ���2����CB�ϣ���3����BA�ϣ����Ĵ����������ڵ�D�ϣ���2Ȧ��2����D��������D�㿪ʼ����һֱ�����ң���˵�5��������Ȼֻ���Ǽױ��Ҷ�����һȦ��
�ҵ�ƽ���ٶ�=��90+90���£�90��6+90��4��=4.8����/�룩
��ʱ����£�360�£�5��4.8��=1800���룩
������1800��5��360=25��Ȧ��
������1800��75=24��Ȧ��
���Ե�5������֮��2�˻����֮ǰ�Ĺ��̣��ʵ�100������ʱ��Ϊ��
1800��20=360000���룩���ص���A��
�𣺳�����360000�����ǵ�100�������������ص��ڵ�A����