Question

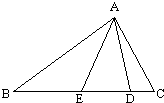在三角ABC中，D，E是BC边上的点，BD=AB，CE=AC，又∠DAE=

1

3

∠BAC，求∠BAC的度数．

Answer 1

分析：设∠BAE，∠EAD，∠DAC分别为α，β，γ，则依据等腰三角形的两个底角的度数相等，以及三角形的内角和定理，即可进行解答．

解答：解：设∠BAE，∠EAD，∠DAC分别为α，β，γ，
则β=

1

3

（α+β十γ），即 2β=α+γ．
由AB=BD得，α+β=∠BDA=γ+∠C，②
由CE=AC得，β+γ=∠CEA=α+∠B，③
②十③得，α+γ+2β=∠B+∠C+α+γ，④
两边再加上β得，α+γ+3β=∠B+∠C+∠BAC=180°⑤
由于①上式即，5β=180°
所以3β=

180°

5

×3=108°，
即∠BAC=108°．

点评：此题主要考查等腰三角形的特点以及三角形的内角和定理．