Question

6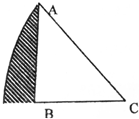．一个等腰直角三角形ABC的面积是20平方厘米，阴影部分的面积是多少？

Answer 1

分析 根据图形可得：阴影部分的面积=这个$\frac{1}{4}$圆的面积-正方形ABCD的面积，连接正方形的对角线AC，BD，根据正方形的对角线的特点可得：AO=CO=BO=OD=半径的一半，得到四个全等的直角三角形，三角形ABC的面积已知，于是可以求出圆的半径的平方值，于是问题即可得解．

解答 解：据分析可得：
设圆的半径为r，
则$\frac{r}{2}$×$\frac{r}{2}$×$\frac{1}{2}$×4=20×2
           $\frac{{r}^{2}}{4}$=20
           r²=80
所以阴影部分的面积为：
$\frac{1}{2}$×（3.14×80×$\frac{1}{4}$-20×2）
=$\frac{1}{2}$×（62.8-40）
=11.4（平方厘米）
答：阴影部分的面积是11.4平方厘米．

点评 本题主要考查组合图形的面积，求出圆的半径的平方值，是解答本题的关键．