题目内容
11.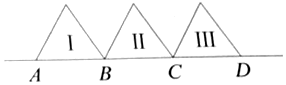 如图,一条直线上放着一个边长为3cm的等边三角形Ⅰ,让这个等边三角形Ⅰ绕顶点B顺时针旋转120°后到达等边三角形Ⅱ的位置,这样连续做两次,点A到达点D的位置,求点A走过的路程的长(结果保留π)
如图,一条直线上放着一个边长为3cm的等边三角形Ⅰ,让这个等边三角形Ⅰ绕顶点B顺时针旋转120°后到达等边三角形Ⅱ的位置,这样连续做两次,点A到达点D的位置,求点A走过的路程的长(结果保留π)
分析 等边三角形Ⅰ绕顶点B顺时针旋转120°后到达等边三角形Ⅱ的位置,A点走过的路程是以一边长3厘米圆心角为120°的弧长,连续做两次A点走过的路程是以一边长3厘米圆心角为120°×2=240°的弧长,根据根据l=2×$\frac{n}{360}$πr
解答 解:2×$\frac{120×2}{360}$π×2
=2×$\frac{2}{3}$π×2
=$\frac{8}{3}$π(厘米)
答:A走过的路程的长是$\frac{8}{3}$π厘米.
点评 本题的重点是让学生理解A点走过路程的轨迹,再根据弧长的计算公式进行计算.

练习册系列答案
相关题目
2.一件羽绒服先涨价20%,再降价20%,现在的价钱与原来相比,( )
| A. | 原价多 | B. | 现价多 | C. | 同样多 | D. | 无法确定 |
6.在下图中,以直线为轴旋转,可以得出得出圆锥体的是( )
| A. |  | B. |  | C. |  | D. |  |
7.6.7×99可以用( )律进行简算.
| A. | 乘法交换 | B. | 乘法结合 | C. | 乘法分配 |