题目内容
扑克牌中的J、Q、K分别表示11、12、13.甲取13张红心,乙取13张草花,两人都各自任意出一张牌凑成一对,这样一共可凑成13对.如果将每对求和,再将这13个和相乘.从积的奇偶性看,积应是
偶
偶
数.分析:1,2,3,4,5,6,7,8,9,10,11,12,13这13个数字中,任意取两个数求和,每个数可重复取两次,结果应该是偶数,因为:在奇数个数中,不管怎么配对,总会有两个数的和是偶数.因为奇+偶=奇,奇+奇=偶,在奇数个数中,任取一奇一偶,加起来是奇数,但会多一个数没有配对,在下一轮中,同样有一个没有配对,剩下的必是一个奇数,两个奇数加起来必是偶数.只要有一个偶数,则乘积必是偶数.
解答:解:在1至13中,有6个偶数,7个奇数,任意取两个数求和,根的数的奇偶性,不管怎么配对,总会有两个数的和是偶数.
所以,只要有一个偶数,则乘积必是偶数.
故答案为:偶.
所以,只要有一个偶数,则乘积必是偶数.
故答案为:偶.
点评:根据数的奇偶性可知:奇+偶=奇,奇+奇=偶,偶×奇=偶.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 ①每张牌都是A、K、Q、J中的某一张;
①每张牌都是A、K、Q、J中的某一张;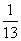 ,他说得对吗?
,他说得对吗?