Question

Answer 1

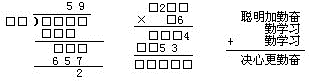
分析：（1）题中根据商的个位数字是9，除数与9的积是657，确定除数是73；根据余数是2，确定被除数的个位数字是9，除数是73，商的十位数字是5，计算出商的十位数字与除数的积，进而确定除数的千位数字、百位数字、十位数字，写出整个算式．
（2）题根据第二个因数与第一个因数个位数字相乘积的个位数字是4，推测第一个因数个位数字是4或9，结合第二个因数十位上的数字与第一个因数的积的个位数字是3确定第一个因数个位数字是9；进而确定第二个因数的十位数字是7；根据第二个因数十位数字与第一个因数的积的十位数字是5，确定第一个因数十位数字是7；又因第二个因数十位数字与第一个因数的积是四位数，确定第一个因数千位数字是1；最后写出整个算式．
（3）题根据三个加数个位数：奋+习+习=奋可以确定习可能是0或5，再根据十位数：勤+学+学=勤可以确定个位数所加的和没有向十位进1，所以习=0；根据十位上勤+学+学=勤确定学=5；千位上只有一个数相加，所得的和与原来的数不同，说明百位上的数向千位上进了1或2，如果百位向千位进1，千位上最大可能是9，千位上的和就应为0，与前面确定的习=0相矛盾，所以百位应该向千位进2，千位上应该是最大的一位数，从而确定明=9，心=1；因为百位的和向千位进2，所以加和勤应该是比较大的数，根据算式中数字不重复的原则，确定勤=7，加=8，更=2；根据进位的原则判断决比聪大1，确定聪=3，决=4；最后确定奋=6．

解答：解：答案如下：

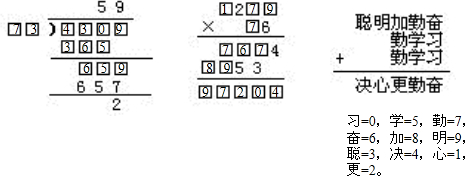
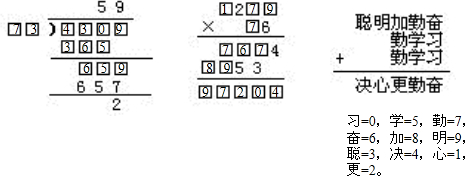
点评：此题难度较大，解答此题根据进位原则和数字不重复的原则进行解答．