题目内容
10月1目是国庆节，右图是“10.1”两个数，请把l～18这18个数填入图中的18个空格内，使每一横行与竖行上所填的数的和都相等．
分析：在填这个封闭型数阵的过程中，显然，中间的“0”的四个顶点上的数与每个笔划上所填数的和是关键，故设四个顶点上的数分别是a、b、c、d，每个笔划上所填数的和都是k，如图：
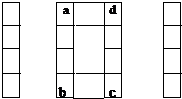
可以看出：
6k=（1+2+3+…+18）+（a+b+c+d）
讨论此时k的取值即可．
可以看出：
6k=（1+2+3+…+18）+（a+b+c+d）
讨论此时k的取值即可．
解答：解：设四个顶点上的数分别是a、b、c、d，每个笔划上所填数的和都是k，那么：6k=（1+2+3+…+18）+（a+b+c+d），
6k=171+a+b+c+d，
k=（171+a+b+c+d）÷6，
a+b+c+d=6k-171；
当a+b+c+d 取最小值10时，
k=（171+10）÷6=30.16，
所以k的最小值是31，当a+b+c+d取最大值66时，
k=（171+66）÷6=39.5，所以k的最大值是39．
因此k=31，32，33，34，…38，39．
下面试验求解：
（1）当k=34时，得a+b+c+d=6×34-171=33
因为6+8+9+10=33，经试验可知，当a=6，b=8，c=9，d=10时，可得到一个基本解如下图：
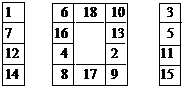
（2）当k=35时，由a+b+c+d=6k-171得：
a+b+c+d=6×35-171=39，
因为5+6+12+16=39，经试验可知，当a=5，b=6，c=12，d=16时，可得到一个基本解，如下图：
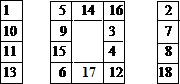
还可以再取k为其他值，得到其它答案．
6k=171+a+b+c+d，
k=（171+a+b+c+d）÷6，
a+b+c+d=6k-171；
当a+b+c+d 取最小值10时，
k=（171+10）÷6=30.16，
所以k的最小值是31，当a+b+c+d取最大值66时，
k=（171+66）÷6=39.5，所以k的最大值是39．
因此k=31，32，33，34，…38，39．
下面试验求解：
（1）当k=34时，得a+b+c+d=6×34-171=33
因为6+8+9+10=33，经试验可知，当a=6，b=8，c=9，d=10时，可得到一个基本解如下图：
（2）当k=35时，由a+b+c+d=6k-171得：
a+b+c+d=6×35-171=39，
因为5+6+12+16=39，经试验可知，当a=5，b=6，c=12，d=16时，可得到一个基本解，如下图：
还可以再取k为其他值，得到其它答案．
点评：本题关键是找出重复的数字的值，然后进行求解．
练习册系列答案
相关题目