题目内容
 两个直角三角板如图放置,则∠BFE的度数是∠CAF的
两个直角三角板如图放置,则∠BFE的度数是∠CAF的9
9
倍.分析:首先根据直角三角形的两锐角互余,求得∠BAC与∠BAE的度数,由∠ABC=∠D=90°,可得BC∥DE,可求得∠BFE的度数,问题则可得解.
解答:解:因为在Rt△ADE中,∠E=45°,∠D=90°,
所以∠DAE=90°-∠E=45°,
因为在Rt△ABC中,∠C=30°,∠ABC=90°,
所以∠BAC=90°-∠C=60°,
所以∠D=∠ABC,∠FAC=∠BAC-∠BAE=60°-45°=15°,
所以BC∥DE,
所以∠BFE+∠E=180°,
所以∠BFE=135°,
所以∠BFE÷∠CAF=135°÷15°=9.
故答案为:9.
所以∠DAE=90°-∠E=45°,
因为在Rt△ABC中,∠C=30°,∠ABC=90°,
所以∠BAC=90°-∠C=60°,
所以∠D=∠ABC,∠FAC=∠BAC-∠BAE=60°-45°=15°,
所以BC∥DE,
所以∠BFE+∠E=180°,
所以∠BFE=135°,
所以∠BFE÷∠CAF=135°÷15°=9.
故答案为:9.
点评:此题考查了直角三角形的两锐角互余的性质与平行线的性质与判定.解此题的关键是要注意合理应用数形结合思想.

练习册系列答案
相关题目
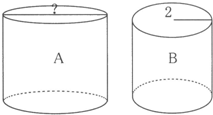 龙博士有两个容器(如图所示),原来A容器中装有2000毫升的水,B容器是空的.现在以每分钟400 毫升的流量往两个容器里注入水,4分钟后,两个容器水面高度相等.已知B容器的底面半径是2厘米,则A容器的底面直径是多少?
龙博士有两个容器(如图所示),原来A容器中装有2000毫升的水,B容器是空的.现在以每分钟400 毫升的流量往两个容器里注入水,4分钟后,两个容器水面高度相等.已知B容器的底面半径是2厘米,则A容器的底面直径是多少? 一个梯形中有两个直角,一条线段把梯形分成两个三角形(如图),三角形①是
一个梯形中有两个直角,一条线段把梯形分成两个三角形(如图),三角形①是 将分别含有30°和45°角的一副三角板如图放置,且30°和45°角的顶点重合在一起,OM平分∠AOC,ON平分∠DOC,画出几何图形,并求∠MON的大小.
将分别含有30°和45°角的一副三角板如图放置,且30°和45°角的顶点重合在一起,OM平分∠AOC,ON平分∠DOC,画出几何图形,并求∠MON的大小. 如图,将两个有一个角是60°的同样的直角三角板如图放置.如果三角板的斜边长0.1dm,图中阴影部分的面积是多少平方厘米?
如图,将两个有一个角是60°的同样的直角三角板如图放置.如果三角板的斜边长0.1dm,图中阴影部分的面积是多少平方厘米?