题目内容
这是一块正方形的地板砖示意图.其中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,红色小正方形的面积是4,绿色的四块面积总和是18.求这个大正方形ABCD的面积,请说明理由.
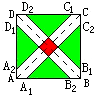

根据题干分析可得:如上图所示,右边围成的绿色小正方形的面积是18÷2=9,
又因为3×3=9,所以绿色小正方形的边长是3;
中间红色小正方形的面积是4,则大正方形的两条对角线把红色小正方形平均分成四个完全相同的小正方形,每个红色小正方形的面积是4÷4=1,则红色小正方形的边长是1,
所以右边虚线围成的大正方形的边长是3+1+1=5,
则可得它的面积是5×5=25,
所以原正方形的面积是25×2=50.
答:大正方形ABCD的面积是50.
又因为3×3=9,所以绿色小正方形的边长是3;
中间红色小正方形的面积是4,则大正方形的两条对角线把红色小正方形平均分成四个完全相同的小正方形,每个红色小正方形的面积是4÷4=1,则红色小正方形的边长是1,
所以右边虚线围成的大正方形的边长是3+1+1=5,
则可得它的面积是5×5=25,
所以原正方形的面积是25×2=50.
答:大正方形ABCD的面积是50.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目