题目内容
已知A、B分别是正方形相邻两条边上的中点，阴影部分的面积占整个图形面积的
．
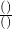解：用图表示如下：
[2×2-（1×1÷2+2×1÷2+2×1÷2）]÷（2×2），
=[4-2.5]÷4，
=1.5÷4，
=
；
答：阴影部分的面积占整个图形面积的．
故答案为：．
分析：我们假设正方形的边长是2，分别求出3个直角三角形的面积，用正方形的面积减去就是阴影部分的面积，再用三角形的面积除以正方形的面积就是阴影部分的面积占整个图形面积几分之几．
点评：运用正方形的面积及三角形的面积公式进行解答，即，正方形的面积=边长×边长，底×高÷2=三角形的面积．
[2×2-（1×1÷2+2×1÷2+2×1÷2）]÷（2×2），
=[4-2.5]÷4，
=1.5÷4，
=
；答：阴影部分的面积占整个图形面积的
．故答案为：
．分析：我们假设正方形的边长是2，分别求出3个直角三角形的面积，用正方形的面积减去就是阴影部分的面积，再用三角形的面积除以正方形的面积就是阴影部分的面积占整个图形面积几分之几．
点评：运用正方形的面积及三角形的面积公式进行解答，即，正方形的面积=边长×边长，底×高÷2=三角形的面积．
练习册系列答案
相关题目
已知A、B分别是正方形相邻两条边上的中点，阴影部分的面积占整个图形面积的有四个均不为零的数，分别是a、b、c、d，已知a＞b＞c＞d．若四个数能组成比例，一定有（ ）
| A、ab=cd | B、ad=bc | C、ac=bd |