Question

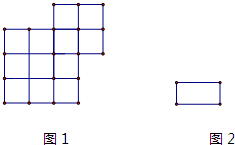图1中的每个方格边长是1分米，现在有6块长2分米、宽1分米的木板（见图2），问有多少种不同的方法可将这6块木板覆盖图1这个图形（任何两块木板不能重叠）？请做出图示．

Answer 1

分析：观察图形可知，右上边有两种不同的方法，左下边有4种不同的方法，再根据乘法原理即可求解．

解答：解：由图形可知，右上边有两种不同的方法，左下边有4种不同的方法，
2×4=8（种）．
答：有8种不同的方法．

点评：考查了简单图形覆盖现象中的规律，本题分右上边的正方形和左下边的图形分别计数求解．