Question

如图中16格内填的都是由1、6、8、9组成的两位数．并且横行、竖行和对角线上四个数的和都相等．则快=

69

，乐=

91

，数=

86

，学=

18

．

Answer 1

分析：根据双偶数阶幻方的制作的对称性可知：“快”原来在“学”的位置，“乐”原来在“数”的位置，（原图如下）；因此可得：乐=快+1，数=快+4，学=快+5，“快”原来左面的数是“快”-1，“乐”右面的数是“快”+2，根据幻和横行、竖行和对角线上四个数的和都相等即和为：96+11+89+68=264，可得：（快-1）+学+数+（快+2）=（快-1）+（快+5）+（快+4）+（快+2）=264，得出“快”=69，进而可得：“学”=18，“数”=86，“乐”=91，然后填空即可．

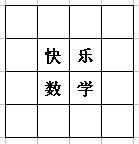
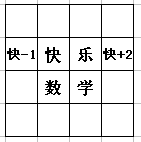
解答：解：根据分析可得，乐=快+1，数=快+4，学=快+5，
（快-1）+学+数+（快+2）=264，
（快-1）+（快+5）+（快+4）+（快+2）=264，
解得：“快”=69，
“学”=18，“数”=86，“乐”=91，
故答案为：69，91，86，18．

点评：本题考查了双偶数阶幻方制作的逆推导，关键是根据它的对称性、幻和、数字间的关系先确定其中的一个数；实际上中间四个数的和就等于幻和，同学们可以记住这个结论直接解答．