Question

【题目】、两地相距千米．有一支游行队伍从出发，向匀速前进；当游行队伍队尾离开时，甲、乙两人分别从、两地同时出发．乙向步行；甲骑车先追向队头，追上队头后又立即骑向队尾，到达队尾后再立即追向队头，追上队头后又立即骑向队尾……当甲第次追上队头时恰与乙相遇在距地千米处；当甲第次追上队头时，甲恰好第一次到达地，那么此时乙距地还有多少千米？

Answer 1

【答案】14.4千米

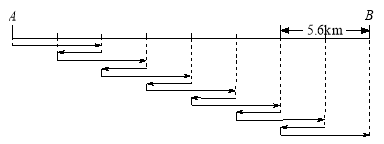
【解析】整个行程如图所示．设甲第一次追上队头与第二次追上队头时队伍所行的距离为千米，第一次从队头到队尾时甲所行距离为千米．由于每一次甲都是从队尾追上队头，再从队头回到队尾，追上队头是一个追及过程，回到队尾是一个相遇过程，而追及、相遇的路程都是队伍的长度，队伍的长度是不变的，所以每一次追及、相遇的时间也是不变的，所以每一次甲追上队头到下一次甲追上队头这段时间内队伍所行的路程(即图中相邻两条虚线之间的距离)都是相同的，而每一次从队头到队尾时甲所行的路程也都是相同的．

根据题意，甲第5次追上队头时距地5.6千米，第7次追上队头时恰好到达地，所以；从图中可以看出，，所以：，解得．

甲第5次追上队头时恰与乙相遇在距地5.6千米处，甲第5次追上队头时共行了

千米，根据时间一定，速度比等于路程之比，可得．

从甲第5次追上队头到甲第7次追上队头，甲共行了千米，所以这段时间内乙行了千米，所以此时乙距地还有(千米)．