题目内容
2.如图,正方形ABCD的面积是72平方厘米,CD=3EF,则两块阴影部分相差6平方厘米.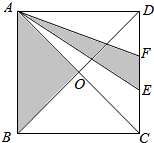
分析 先求出两块阴影部分的面积,根据题意,△AOB的面积为正方形面积的$\frac{1}{4}$,用正方形的面积除以4就是,△AOB的面积;因为CD=3EF,所以△AEF的面积是△ACD面积的$\frac{1}{3}$,而△AEF的面积是正方形面积的一半,因此,用正方形的面积除以2再除以3,即可求出△AEF的面积.
解答 解:△AOB的面积为:
72÷4=18(平方厘米)
△AEF的面积为:
72÷2÷3
=36÷3
=12(平方厘米)
二者相差:
18-12=6(平方厘米)
答:两块阴影部分相差6平方厘米.
故答案为:6.
点评 此题解答的关键在于根据阴影部分与正方形之间的面积关系,求得两部分的阴影面积,进而解决问题.

练习册系列答案
相关题目