题目内容
（1）
÷[1÷（1.6-1.599）]
（2）[
÷
-（
+
）]÷
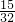
（3）99×
（4）1-
+
-
+
-
+
-
．
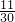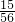解：（1）÷[1÷（1.6-1.599）]，
=÷[1÷0.001]，
=÷1000，
=
；
（2）[÷-（+）]÷，
=[÷-
]÷，
=[
-]÷，
=
×
，
=
；
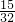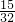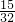（3）99×，
=（98+1）×，
=98×+1×，
=97+，
=97；
（4）1-+-+-+-，
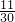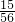=1-（
+
）+（+）-（-
）-…-（
+
），
=1--++---…--，
=1--，
=-，
=
．
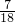分析：（1）先算小括号里面的减法，再算中括号里面的除法，最后算括号外的除法；
（2）先算小括号里面的加法，再算中括号里面的除法，然后算中括号里面的减法，最后算括号外的除法；
（3）先把99分解成98+1，再运用乘法分配律简算；
（4）通过观察发现这些分数有一定的特点，分子与分子、分母与分母都按一定的规律递增，并且每一个分数都能拆成两个分数相加的形式，所以我们就进行分数的拆项，拆项后，通过前后两个分数相互抵消，达到简算的目的．
点评：本题考查了四则混合运算，注意运算顺序和运算法则，灵活运用所学的运算定律进行简便计算．
÷[1÷（1.6-1.599）]，=
÷[1÷0.001]，=
÷1000，=
；（2）[
÷-（+）]÷，=[
÷-]÷，=[
-]÷，=
×，=
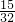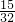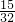；（3）99×
，=（98+1）×
，=98×
+1×，=97+
，=97
；（4）1-
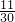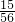+-+-+-，=1-（
+）+（+）-（-）-…-（+），=1-
-++---…--，=1-
-，=
-，=
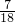．分析：（1）先算小括号里面的减法，再算中括号里面的除法，最后算括号外的除法；
（2）先算小括号里面的加法，再算中括号里面的除法，然后算中括号里面的减法，最后算括号外的除法；
（3）先把99分解成98+1，再运用乘法分配律简算；
（4）通过观察发现这些分数有一定的特点，分子与分子、分母与分母都按一定的规律递增，并且每一个分数都能拆成两个分数相加的形式，所以我们就进行分数的拆项，拆项后，通过前后两个分数相互抵消，达到简算的目的．
点评：本题考查了四则混合运算，注意运算顺序和运算法则，灵活运用所学的运算定律进行简便计算．
练习册系列答案
相关题目
三种形式组成的图形，并在每个小方格全部加1或减1，如此反复多次进行形成的，试问（表2）中的A格上的数字是多少？并说明理由．
| 1.23÷3= | 0.8×11= | 1-0.75= |
| 1.7×0.4= | 0.36÷12= | 1.6+0.38= |
| 1.2÷0.3= | 0.75×4= | 15×0.4= |
| 2.14-0.9= | 4×0.25= | 10÷2.5= |
| 0.4×52= | 1.6×0.4= | 9.6÷6= |
| 4.3-0.4= | 7-6.2= | 0.86-0.3= |
| 8.8÷2.2= | 2.6÷0.2= | 0.15×3= |
| 0.9÷0.45= | 0.27÷3= | 0.51+1.7= |
| 0.6÷0.5= | 0.125×8= | 0.38×1000= |
| 6.8-1.7= | 2.4×0.2= | 32.8+19= |
| 0.56÷14= | 1÷0.05= | 6÷12= |
| 0.14×5= | 3×1.4= | 4.9÷0.7= |
| 0.4÷8= | 6.3+3.7= | 3.5×0.2= |
| 0.2×12.6×5= | 8.4÷4.2= | 2.4×0.5= |
| 0÷3.5×0.2= | 0×9.7+2.3= | 1.6×9+1.6= |
| 3.8+1.2= | 4.8÷0.3= | 530+270= |
| 7.6÷3.8= | 92÷2.3= | 9.6-1.6= |
| 7.2+2.8= | 2.63+0.37= | 0.67+1.24= |
| 0.3×101= | 0.25×8= | 16÷1.6= |
| 26.1-3.5-7.5= |
| 在一次校运动会中，参加甲组跳高的36名运动员的成绩如下：（单位：米） 1. 15 1.10 1.05 1.10 0.90 1.10 1.20 0.80 1.10 1. 20 1.10 1.15 1.20 0.90 1.10 0.85 1.05 0.90 0. 95 0.85 1.10 0.95 1.15 1.10 1.05 1.00 1.00 1. 10 0.80 1.10 1.00 0.90 0.95 1.05 1.10 1.10 （1）整理上面的数据，将表格填写完整。
（3）这组运动员的平均成绩是（ ）米。 |