Question

如图，把△ABC滚到△A′B′C′的位置．求△ABC滚动过的面积．（注：圆周率取3.14）

Answer 1

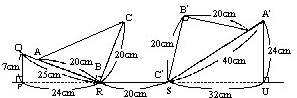
分析：画出△ABC滚动到△A′B′C′的位置时滚动的轨迹图，如下图所示．因此△ABC滚动过的面积可分成三部分：第一部分是以R为圆心，三角形的直角边为半径的扇形①；第二部分即三角形ABC②；第三部分是以S为圆心，三角形的斜边为半径的扇形（③+④）．设出各圆心角的度数如图所示，即可表示出图中①、②、③、④部分的面积；分割三角形suf，易知分出的三个三角形都是直角三角形，结合勾股定理以及y°×2+x°=180°，即可求出各部分的面积和，从而得出△ABC滚动过的面积．

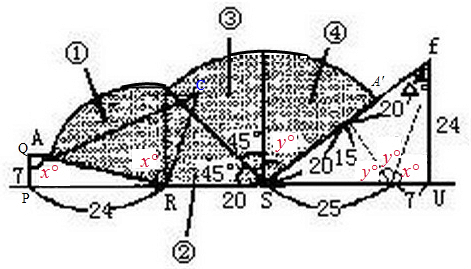
解答：解：画出△ABC滚动到△A′B′C′的位置时滚动的轨迹图，如上图所示，
①部分的面积为：

x

360

×3.14×20²，
②部分的面积为：

1

2

×20×20=200，
③部分的面积为：

45

360

×3.14×AC²，
④部分的面积为：

y

360

×3.14×AC²，
由勾股定理可知：AC²=AB²+BC²=20²+20²=800，
分割三角形suf（见上图），可知分出的三个三角形都是直角三角形，y°×2+x°=180°．
由于②+③=200+

45

360

×3.14×AC²
=200+

45

360

×3.14×800
=200+314
=514；
①+④=

x

360

×3.14×20²+

y

360

×3.14×AC²
=

x

360

×3.14×400+

y

360

×3.14×800
=400×3.14×

x+2y

360

=400×3.14×

180

360

=628；
所以△ABC滚动过的面积是：514+628=1142（cm²）．
答：△ABC滚动过的面积是1142cm²．

点评：本题解决的关键是能够明确三角形滚过的区域由哪些图形构成，然后用图形的面积公式解决．另外用到了勾股定理及平角的定义等知识以及整体代入的数学思想方法．