题目内容
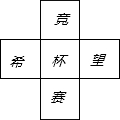
将2005,2006,2007,2008,2009这5个数分别填入图中写有“希望杯竞赛”的五个方格内,使得:希+望+杯=竞+赛+杯,则共有
24
24
种不同的填法.
分析:假设“杯”所在的数是a,希+望+杯=竞+赛+杯=k,则有:2005+2006+2007+2008+2009+a=2k,代入不同的a,对应不同的k值,即可得解.
解答:解:2005+2006+2007+2008+2009+a=2k,
a=2005时,k=6020,6020-2005=4015,希望是2006、2009,则竞赛是2007、2008,2×2=4种填法,或者竞赛是2007、2008,希望是2006、2009,2×2=4种填法,共有8种填法;
其他a=2006,和不能被2整除,无解;
a=2007,k=6021,6021-2007=4014,希望是2006、2008,则竞赛是2005、2009,2×2=4种填法,或者竞赛是2005、2009,希望是2006、2008,2×2=4种填法,共有8种填法;
a=2008,和不能被2整除,无解;
a=2009,k=6022,6022-2009=4013,希望是2006、2007,则竞赛是2005、2008,2×2=4种填法,或者竞赛是2006、2007,希望是2005、2008,2×2=4种填法,共有8种填法;
8+8+8=24;
答:则共有 24种不同的填法.
故答案为:24.
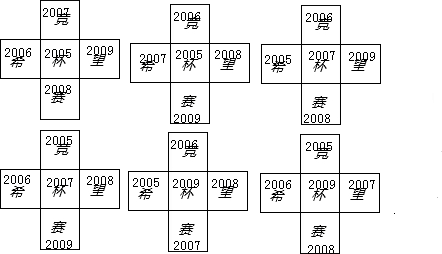
如上图,每一图把“希”和“望”,“竟”和“赛”位置互换,都有4种,不再一一列出.
a=2005时,k=6020,6020-2005=4015,希望是2006、2009,则竞赛是2007、2008,2×2=4种填法,或者竞赛是2007、2008,希望是2006、2009,2×2=4种填法,共有8种填法;
其他a=2006,和不能被2整除,无解;
a=2007,k=6021,6021-2007=4014,希望是2006、2008,则竞赛是2005、2009,2×2=4种填法,或者竞赛是2005、2009,希望是2006、2008,2×2=4种填法,共有8种填法;
a=2008,和不能被2整除,无解;
a=2009,k=6022,6022-2009=4013,希望是2006、2007,则竞赛是2005、2008,2×2=4种填法,或者竞赛是2006、2007,希望是2005、2008,2×2=4种填法,共有8种填法;
8+8+8=24;
答:则共有 24种不同的填法.
故答案为:24.

如上图,每一图把“希”和“望”,“竟”和“赛”位置互换,都有4种,不再一一列出.
点评:此题考查了凑数谜,列出等式,凑数,即可得解.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
王叔叔开了两家一样的商店,两家商店每年的费用基本相同.两家商店2003年至2006年获得利润情况如下表:
| 年份利润(万元)点名 | 2003年 | 2004年 | 2005年 | 2006年 |
| 甲商店 | 20 | 17 | 16 | 14 |
| 乙商店 | 12 | 15 | 18 | 20 |
(2)甲商店2006年获得的利润比2005年减少______%;乙商店2003年至2006年平均每年获得利润______万元.
(3)王叔叔准备关闭其中的一家商店,你认为应关闭______家商店.


