题目内容
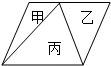 如图,三角形甲的面积是丙面积的
如图,三角形甲的面积是丙面积的| 1 | 3 |
1:2
1:2
,平行四边形的面积是60
60
平方厘米.分析:因为三角形的面积是与其等底等高的平行四边形面积的一半,于是可得:S甲+S乙=S丙=
S平行四边形,又因三角形甲的面积是丙面积的
,三角形乙的面积是20cm2,则三角形乙的面积是三角形丙的面积的1-
=
,于是依据比的意义,及分数除法的意义即可得解.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
解答:解:由题意可得:S甲+S乙=S丙=
S平行四边形,
S甲:S乙=
:(1-
)=
:
=1:2,
20÷(1-
)×2,
=20÷
×2,
=60(平方厘米),
答:甲和乙的面积比是1:2,平行四边形的面积是60平方厘米.
故答案为:1:2;60.
| 1 |
| 2 |
S甲:S乙=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
20÷(1-
| 1 |
| 3 |
=20÷
| 2 |
| 3 |
=60(平方厘米),
答:甲和乙的面积比是1:2,平行四边形的面积是60平方厘米.
故答案为:1:2;60.
点评:解答此题的主要依据是:三角形的面积是与其等底等高的平行四边形面积的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,这两组图形都是由边长为10厘米和4厘米的两个正方形组成,图中三角形甲的面积( )三角形乙的面积.
如图,这两组图形都是由边长为10厘米和4厘米的两个正方形组成,图中三角形甲的面积( )三角形乙的面积. 如图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,三角形ABC是直角三角形,求BC的长.
如图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,三角形ABC是直角三角形,求BC的长.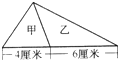 (2007?淮阴区模拟)如图,三角形甲的面积比三角形乙的面积少3平方厘米,甲乙两三角形的面积和是
(2007?淮阴区模拟)如图,三角形甲的面积比三角形乙的面积少3平方厘米,甲乙两三角形的面积和是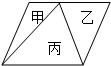 如图,三角形甲的面积是丙面积的
如图,三角形甲的面积是丙面积的 ,三角形乙的面积是20cm2,甲和乙的面积比是________,平行四边形的面积是________平方厘米.
,三角形乙的面积是20cm2,甲和乙的面积比是________,平行四边形的面积是________平方厘米.