题目内容
在两个箱子内，分别有写着0、1、2、3、4、5六个数字的6个相同的小球，从每个箱内各任取1个小球，则两数之和等于7的可能性为多少？两数之和为偶数的可能性为多少？两数之和为3的倍数的可能性是多少？
解：根据题意列表得：
一共有36种情况，两数之和等于7的有共6种情况，可能性：6÷36=
；
两数之和为偶数的有18种情况，可能性：18÷36=
；
两数之和为3的倍数的有11种情况，可能性：11÷36=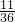
；
答：则两数之和等于7的可能性为，两数之和为偶数的可能性为，两数之和为3的倍数的可能性为．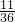
分析：在两个箱子内，分别有写着0、1、2、3、4、5六个数字的6个相同的小球，从每个箱内各任取1个小球，共有36种情况，则两数之和等于7的有（1、6）、（2、5）、（3、4）、（4、3）、（5、2）、（6、1）共6种情况；两数之和为偶数的有18种情况；两数之和为3的倍数的有11种情况；然后根据可能性的求法：求一个数是另一个数的几分之几，用除法分别解答即可．
点评：关键是列举出所有情况，易错点是得到所求情况数；用到的知识点：可能性的求法：求一个数是另一个数的几分之几，用除法解答．
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | （1，1） | （1，2） | （1，3） | （1，4） | （1，5） | （1，6） |
| 2 | （2，1） | （2，2） | （2，3） | （2，4） | （2，5） | （2，6） |
| 3 | （3，1） | （3，2） | （3，3） | （3，4） | （3，5） | （3，6） |
| 4 | （4，1） | （4，2） | （4，3） | （4，4） | （4，5） | （4，6） |
| 5 | （5，1） | （5，2） | （5，3） | （5，4） | （5，5） | （5，6） |
| 6 | （6，1） | （6，2） | （6，3） | （6，4） | （6，5） | （6，6） |
；两数之和为偶数的有18种情况，可能性：18÷36=
；两数之和为3的倍数的有11种情况，可能性：11÷36=
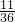；答：则两数之和等于7的可能性为
，两数之和为偶数的可能性为，两数之和为3的倍数的可能性为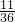．分析：在两个箱子内，分别有写着0、1、2、3、4、5六个数字的6个相同的小球，从每个箱内各任取1个小球，共有36种情况，则两数之和等于7的有（1、6）、（2、5）、（3、4）、（4、3）、（5、2）、（6、1）共6种情况；两数之和为偶数的有18种情况；两数之和为3的倍数的有11种情况；然后根据可能性的求法：求一个数是另一个数的几分之几，用除法分别解答即可．
点评：关键是列举出所有情况，易错点是得到所求情况数；用到的知识点：可能性的求法：求一个数是另一个数的几分之几，用除法解答．
练习册系列答案
考前必练系列答案
相关题目