题目内容
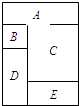 如图,把A、B、C、D、E这个五部分用四种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相领的部分可以使用同一种颜色.那么这幅图一共有多少种不同的着色方法?
如图,把A、B、C、D、E这个五部分用四种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相领的部分可以使用同一种颜色.那么这幅图一共有多少种不同的着色方法?分析:按A,B,C,D,E的顺序,A有4种选择;因为B不能与A同色,所以B有3种选择;因为C不能与A、B同色,所以C有2种选择;因为D不能与BC、同色,所以D有2种选择;因为E不能与D、C同色,所以E有2种选择;故共有:3×3×2×2×2=72(种).
解答:解:按A,B,C,D,E的顺序,分别有4,3,2,2,2种颜色可选,
所以不同颜色着色方法共有4×3×2×2×2=96(种).
答:这幅图一共有96种不同的着色方法.
所以不同颜色着色方法共有4×3×2×2×2=96(种).
答:这幅图一共有96种不同的着色方法.
点评:此题考查了学生有关排列以及组合等知识.

练习册系列答案
相关题目
 如图,把A,B,C,这三部分用五种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色.那么,这幅图一共有( )种不同的着色方法.
如图,把A,B,C,这三部分用五种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色.那么,这幅图一共有( )种不同的着色方法.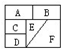 如图,把A,B,C,D,E,F这六个部分用5种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,那么这幅图一共有
如图,把A,B,C,D,E,F这六个部分用5种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色,那么这幅图一共有
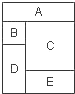 如图,把A,B,C,D,E这五部分用四种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色.那么,这幅图一共有
如图,把A,B,C,D,E这五部分用四种不同的颜色着色,且相邻的部分不能使用同一种颜色,不相邻的部分可以使用同一种颜色.那么,这幅图一共有