题目内容
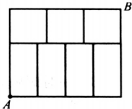 如图,要把棋子从 A 处移到B 处,要求只能向上、向右移动,共有
如图,要把棋子从 A 处移到B 处,要求只能向上、向右移动,共有11
11
种不同的移动路线.
分析:解法一:标上字母,找出所有的路线;
解法二:运用标数法进行求解.
解法二:运用标数法进行求解.
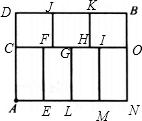
解答:解:解法一:为了叙述的方便,我们在各交叉点标上字母(见图);我们从A点出发,先顺序往上推:
①A-C-D-B;②A-C-F-O-B;③A-C--F-J-B;④A-C-H-K-B;⑤A-C-O-B;
再从A点向右推:①A-E-F-J-B;②A-E-F-H-K-B;③A-L-G-H-K-B;④A-L-G-O-B;⑤A-M-I-O-B;⑥A-N-B.
因此共有:5+6=11(种).
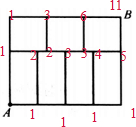
解法二:或见右图,与B点相邻的两个点,经过它们的路线分别有5条和6条,因此共有:5+6=11(条).
所以:要把棋子从 A 处移到B 处,要求只能向上、向右移动,共有 11种不同的移动.
故答案为:11.
①A-C-D-B;②A-C-F-O-B;③A-C--F-J-B;④A-C-H-K-B;⑤A-C-O-B;
再从A点向右推:①A-E-F-J-B;②A-E-F-H-K-B;③A-L-G-H-K-B;④A-L-G-O-B;⑤A-M-I-O-B;⑥A-N-B.
因此共有:5+6=11(种).

解法二:或见右图,与B点相邻的两个点,经过它们的路线分别有5条和6条,因此共有:5+6=11(条).

所以:要把棋子从 A 处移到B 处,要求只能向上、向右移动,共有 11种不同的移动.
故答案为:11.
点评:要按照一定的逻辑次序来排列可能路线,做到不重复,也不遗漏.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目