Question

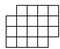如图所示，由14个相同小方格组成的图形，证明不论怎么剪，总不能剪成由相邻的两个小方格组成的7个长方形．

Answer 1

分析：把每个小方格染色，染成黑白相间，发现黑色和白色小方格个数不相等，但是无论怎么剪每个1乘2的小长方形都是一个黑格一个白格所以如果可以剪，那么黑白格子的数量应该相等，但是这里不相等所以不能剪．

解答：解：将这14个小方格黑白相间染色（见下图），

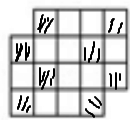
有8个黑格，6个白格．相邻两个方格必然是一黑一白，如果能剪裁成7个小长方形，那么14个格应当是黑、白各7个，与实际情况不符；
所以不能剪裁成7个由相邻两个方格组成的长方形．

点评：如果14小方格组成的是一个规则的长方形的话，就能剪成由相邻的两个小方格组成的7个长方形．