Question

在一个半径为1的圆内，随意放置7个点，证明必有两个点之间距离不超过1．

Answer 1

分析：把圆平均分为六份，分两种情况，情况一：一点在圆心，剩下六点分别在六块的圆弧中点（或圆弧同样位置）上，则每两点距离均为1；情况二：七个点随机分在六块里，由抽屉原理，必有一块至少有两个点，此两点间距离小于1．

解答：解：如图，把圆平均分为六份，分两种情况，

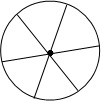
情况一：一点在圆心，剩下六点分别在六块的圆弧中点（或圆弧同样位置）上，则每两点距离均为1；
情况二：七个点随机分在六块里，由抽屉原理，必有一块至少有两个点，此两点间距离小于1；
根据两种情况得出：在一个半径为1的圆内，随意放置7个点，必有两个点之间距离不超过1问题得证．

点评：解答此题应结合题意，分两种情况进行分析，进而得出结论．