题目内容
一个圆柱体如图，另一个与它体积相等、高相等的圆锥体的底面积是________．
84.78平方厘米
分析：要求圆锥体的底面积是圆柱体底面积的几分之几，先根据“圆柱的体积=SH”和“圆锥的体积=
sh”的计算公式进行分析，计算，进而得出结论．
解答：圆柱的体积：v=S1h，
圆锥的体积=S2h，由题意可得：S1h=S2h，
S2=3S1；
即3.14×（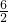
）2×3，
=3.14×9×3，
=84.78（平方厘米）
答：圆锥体的底面积是84.78平方厘米．
故答案为：84.78平方厘米．
点评：此题可结合题意，根据圆柱的体积和圆锥的体积计算公式进行分析、推导，进而得出结论．
分析：要求圆锥体的底面积是圆柱体底面积的几分之几，先根据“圆柱的体积=SH”和“圆锥的体积=
sh”的计算公式进行分析，计算，进而得出结论．解答：圆柱的体积：v=S1h，
圆锥的体积=
S2h，由题意可得：S1h=S2h，S2=3S1；
即3.14×（
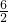）2×3，=3.14×9×3，
=84.78（平方厘米）
答：圆锥体的底面积是84.78平方厘米．
故答案为：84.78平方厘米．
点评：此题可结合题意，根据圆柱的体积和圆锥的体积计算公式进行分析、推导，进而得出结论．
练习册系列答案
相关题目
（2007?延庆县）如图有两张长方形硬纸，请利用这两张硬纸做一个圆柱形纸桶，选用其中一张剪出两个底面，用另一张做侧面，做成的圆柱形纸桶的体积要最大．在你选择做底面的那张硬纸上画出两个底面，然后求出这个圆柱体的体积．（不考虑接缝）
如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图都是同一种几何图形，则另一个几何体是（ ）
| A、长方体 | B、圆柱体 | C、球体 | D、三棱柱 |
如图有两张长方形硬纸，请利用这两张硬纸做一个圆柱形纸桶，选用其中一张剪出两个底面，用另一张做侧面，做成的圆柱形纸桶的体积要最大．在你选择做底面的那张硬纸上画出两个底面，然后求出这个圆柱体的体积．（不考虑接缝）