题目内容
(1)
(2) ×
×
(3) +…+
+…+
(4) ×
× -
- ×
× .
.
解:(1)5 +0.5x=6
+0.5x=6 ,
,
5 +
+ x-5
x-5 =6
=6 -5
-5 ,
,
 x=
x= ,
,
 x×2=
x×2= ×2,
×2,
x= ;
;
(2)(1 ×8.12+5
×8.12+5 ÷
÷ ×8
×8 ),
),
=(1+ )×
)× +(5+
+(5+ )÷
)÷ ×(8+
×(8+ ),
),
=(1+ )×
)× +
+ ×
× ×(8+
×(8+ ),
),
=(1+ )×
)× +
+ ×(8+
×(8+ ),
),
=(1+ +8+
+8+ )×
)× ,
,
=10× ,
,
=81 ;
;
(3) +
+ +
+ +…+
+…+ ,
,
= -
- +
+ -
- +
+ -
- +…+
+…+ -
- ,
,
= -
- ,
,
= ;
;
(4) ×
× -
- ×
× ,
,
设K= +
+ +
+ ,
,
原式=( +K)×(K+
+K)×(K+ )-(k+
)-(k+ +
+ )×K,
)×K,
=K×K+( +
+ )×K+
)×K+ ×
× -K×K-(
-K×K-( +
+ )×K,
)×K,
= ×
× ,
,
=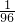 .
.
分析:(1)把0.5化为分数 ,根据等式的性质,两边同减去5
,根据等式的性质,两边同减去5 ,再同乘2即可;
,再同乘2即可;
(2)把8.12化为分数,通过进一步计算,运用乘法分配律简算;
(3)通过观察,此算式的分子都是3,分母中的两个因数相差也是3,可以把每个分数拆分成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
(4)此算式较长,直接计算较麻烦,我们不妨采用设数法,设K= +
+ +
+ ,计算较为简便.
,计算较为简便.
点评:此题考查了解方程以及四则混合运算,解方程时依据等式的性质;在脱式计算中,特别注意运算顺序和运算法则,对分数、小数的互化要细心.根据题目情况,灵活处理.
 +0.5x=6
+0.5x=6 ,
,5
 +
+ x-5
x-5 =6
=6 -5
-5 ,
, x=
x= ,
, x×2=
x×2= ×2,
×2,x=
 ;
;(2)(1
 ×8.12+5
×8.12+5 ÷
÷ ×8
×8 ),
),=(1+
 )×
)× +(5+
+(5+ )÷
)÷ ×(8+
×(8+ ),
),=(1+
 )×
)× +
+ ×
× ×(8+
×(8+ ),
),=(1+
 )×
)× +
+ ×(8+
×(8+ ),
),=(1+
 +8+
+8+ )×
)× ,
,=10×
 ,
,=81
 ;
;(3)
 +
+ +
+ +…+
+…+ ,
,=
 -
- +
+ -
- +
+ -
- +…+
+…+ -
- ,
,=
 -
- ,
,=
 ;
;(4)
 ×
× -
- ×
× ,
,设K=
 +
+ +
+ ,
,原式=(
 +K)×(K+
+K)×(K+ )-(k+
)-(k+ +
+ )×K,
)×K,=K×K+(
 +
+ )×K+
)×K+ ×
× -K×K-(
-K×K-( +
+ )×K,
)×K,=
 ×
× ,
,=
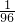 .
.分析:(1)把0.5化为分数
 ,根据等式的性质,两边同减去5
,根据等式的性质,两边同减去5 ,再同乘2即可;
,再同乘2即可;(2)把8.12化为分数,通过进一步计算,运用乘法分配律简算;
(3)通过观察,此算式的分子都是3,分母中的两个因数相差也是3,可以把每个分数拆分成两个分数相减的形式,然后通过加减相抵消的方法,求得结果;
(4)此算式较长,直接计算较麻烦,我们不妨采用设数法,设K=
 +
+ +
+ ,计算较为简便.
,计算较为简便.点评:此题考查了解方程以及四则混合运算,解方程时依据等式的性质;在脱式计算中,特别注意运算顺序和运算法则,对分数、小数的互化要细心.根据题目情况,灵活处理.

练习册系列答案
相关题目
 求图中各个角的度数.已知∠1=75°,∠2=
求图中各个角的度数.已知∠1=75°,∠2=
