题目内容
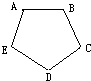 如图是正五边形,已知甲走3份的路程,乙可走5份路程,如果甲、乙同时从A点出发,顺时针走,那么乙第三次追上甲在
如图是正五边形,已知甲走3份的路程,乙可走5份路程,如果甲、乙同时从A点出发,顺时针走,那么乙第三次追上甲在DC
DC
边上.分析:已知甲走3份的路程,乙可走5份路程,即在单位时间内,甲走3条边乙可走5条边即一圈,乙每追上甲1次即要比甲多走1圈,故第3次相遇时,乙共比甲多走了3圈,共多走5×3=15条边. 则第三次追及时,乙已行了15÷(5-3)=7
个时间单位,则此时共行了7
×1=7
圈,则乙第三次追上甲在DC边上.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:三次追及时,乙已行了:3×5÷(5-3)=7
个时间单位,
由于5条边=1圈,
则此时乙共行了7
×1=7
圈,
两人是按A、B、C、D、E、A、…的顺序走的,则第3次相遇地点是在DC边上.
故答案为:DC.
| 1 |
| 2 |
由于5条边=1圈,
则此时乙共行了7
| 1 |
| 2 |
| 1 |
| 2 |
两人是按A、B、C、D、E、A、…的顺序走的,则第3次相遇地点是在DC边上.
故答案为:DC.
点评:此题属于环形跑道的追及问题,明确生追及一次乙就多行一圈并由此求出第三次相遇时乙不行驶的总路程是解题的关键.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目