Question

如图，已知99条直线的交点的最大数目是P，求P的值．

Answer 1

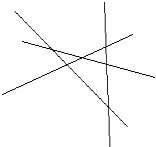
分析：因为两条直线相交，最多有1个交点．三条直线相交，最多有3个交点．四条直线相交，最多有6个交点．五条直线相交，最多有10个交点．…所以n条直线相交，最多有

n(n-1)

2

个交点的个数，再将n=99代入上式即可求得相交点的个数．

解答：解：因为n条直线相交，最多有

n(n-1)

2

个交点；
所以

99×98

2

=4851（个）
答：P的值是4851．

点评：本题是找规律题，找到n条直线相交，最多有有

n(n-1)

2

个交点是解题的关键．