题目内容
(2004?武汉)(1×2×3×4…×50)÷111的商的最后四位数字的和是
0
0
.分析:把111分解质因数是111=3×37,(1×2×3×4…×50)有因数3和37,说明(1×2×3×4…×50)能被111能够整除.整除后的商是(1×2×4×…×36×38×…×50),这个商里仅10×20×30×40×50的积末尾就有6个0,5与偶数相乘还会产生0,因此,商的末尾的0多于6个,因此,(1×2×3×4…×50)÷111的商最后四位数字一定是0,其和也是0.
解答:解:(1×2×3×4…×50)÷111
=(1×2×3×4…×50)÷(3×37)
=1×2×4×…35×36×38×…50
由于1×2×4×…35×36×38×…50
=(10×20×30×40×50)×(1×2×4×…×49)
10×20×30×40×50=12000000,
1×2×4×…×49的积中5与偶数的名人还会有0,
因此(1×2×4×…35×36×38×…50)的末尾要多于6个0,
所以(1×2×3×4…×50)÷111的商的最后四位数字都是0,0+0+0+0=0;
故答案为:0.
=(1×2×3×4…×50)÷(3×37)
=1×2×4×…35×36×38×…50
由于1×2×4×…35×36×38×…50
=(10×20×30×40×50)×(1×2×4×…×49)
10×20×30×40×50=12000000,
1×2×4×…×49的积中5与偶数的名人还会有0,
因此(1×2×4×…35×36×38×…50)的末尾要多于6个0,
所以(1×2×3×4…×50)÷111的商的最后四位数字都是0,0+0+0+0=0;
故答案为:0.
点评:要求(1×2×3×4…×50)÷111的结果很麻烦,关键是看(1×2×3×4…×50)能否被111整除,再确定商的最后四位数,进而求出答案.

练习册系列答案
相关题目
 (2004?武汉)如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米?
(2004?武汉)如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米? (2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天?
(2004?武汉)胡裁缝加工一批服装的情况如图.已知他加工一件童装、一条裤子和一件上衣所需要时间的比是1:2:3,他每天加工2件童装、3条裤子和4件上衣.请问,他加工完这批服装用了多少天?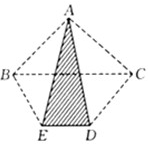 (2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是
(2004?武汉)如图,已知△ABC的面积是2,梯形BCDE的面积是6,并且上底BC是下底DE的2倍,那么△ADE的面积是